# Deep Learning desde 0
> "If you wish to make an apple pie from scratch,
> you must first invent the universe."
>
> -- Carl Sagan, [Cosmos: A Personal Voyage 1980](https://www.youtube.com/watch?v=7s664NsLeFM target="_blank")
¡Hola gente!
Vamos a suponer que sabéis algo de Machine Learning y de Deep Learning. ¿Nunca os habéis preguntado cómo funcionan los Frameworks de Deep Learning? o ¿cómo se prueban nuevas funciones?
Y si no conocéis nada de este apasionante campo, ¿queréis aprender cómo funciona?
Pues si es que sí, creo que estos posts os gustarán.
Si lo que os interesa es coger un dataset de imágenes y clasificarlas, sin calentaros la cabeza.
Estos no son vuestros posts.
Enfocaremos los posts desde el punto de vista de un coder. Hay miles de tutoriales y cursos que nos explican la teoría y matemáticas del Machine Learning y decenas de miles de tutoriales de como usar keras, tensorflow o pytorch.
Aquí vamos a hacer nuestro propio framework de Deep Learning, desde 0.
Pero para eso, no vamos a hablar (por ahora) de redes neuronales.
Durante los primeros posts vamos a tratar, e implementar, temas tan diversos como álgebra, grafos, optimización de funciones,etc.
## ¿Qué necesitamos?
Nuestro lenguaje de programación preferido, paciencia, y solo un poco de python :).
Pero, aparte de eso, lo haremos sin restricciones.
Así que prepárate un buen café (o cerveza) y empecemos.
# ¿Qué es un grafo?.
## Un poco de historia
Allá por el siglo XVIII, en la ciudad de Königsberg (actual Kaliningrado), se formuló un problema matemático que preguntaba si era posible encontrar un recorrido para cruzar toda la ciudad, pasando por todos los puentes una sola vez y regresando al mismo punto de inicio.
En un alarde de originalidad a este problema se le llamó: _Problema de los puentes de Königsberg_
 )]("https://upload.wikimedia.org/wikipedia/commons/5/5d/Konigsberg_bridges.png" target="_blank")
Puedes intentar responder ese problema tu mismo usando la imagen de la ciudad, si quieres :).
Bueno, pues en el año 1736 un matemático conocido como *Leonhard Euler* expuso una solución general al problema y, de paso, creó una nueva rama de las matemáticas llamada Teoría De Grafos.
 )]("https://upload.wikimedia.org/wikipedia/commons/b/b6/EULER_HARLUQ.jpg" target="_blank")
Lo que hizo Euler fue simplificar el mapa de la ciudad a unos puntos (barrios) conectados por unas lineas (puentes) eliminando todo lo sobrante.

Con esta abstracción se deduce que los vértices intermedios deben tener 2 aristas ya que, como solo puedes pasar una vez por cada puente (Arista), si entras a un nodo por una arista debes de salir por otra distinta.
Como en este grafo los puntos poseen un número impar de aristas podemos decir que no se puede resolver el problema de puentes de Königsberg.
Si ya tienes experiencia como programador, ya habrás tratado con grafos y conocerás un poco de teoría de grafos.
!!! Tip
De todas maneras, si no conoces nada de teoría de grafos puedes leer bastante [aquí](https://lmgtfy.com/?q=teoría+de+grafos target="_blank")
En general, podemos ver un grafo como un conjunto de Vértices (o Nodos) conectados por Aristas, donde las aristas conectan Vértices. Son tremendamente útiles para representar información y aplicar distintos algoritmos.
Nosotros vamos a centrarnos en unos tipos particulares de grafos, Grafos Dirigidos, también se suelen llamar _Di-grafos_ .
Un Grafo Dirigido, o Digrafo, es un grafo donde las aristas tienen "dirección", van del nodo A al nodo B, pero no tiene por que ir del nodo B al nodo A.

Un *Grafo Dirigido Acíclico* (DAG) es aquel que no tiene "ciclos". O lo que es lo mismo:
Tomando cualquier nodo del grafo y siguiendo cualquier camino posible, no puedes volver al mismo nodo.
Este es el subtipo de grafos que nosotros vamos a utilizar.

Podemos resumir que un DAG tiene una serie de características básicas:
- Aristas dirigidas: "flechas" en una dirección, de un nodo a otro.
- Nodos: Vértices que almacenan datos o funcionalidad.
- Nodos sin padres: Nodos a los que no llega ninguna "flecha"
- Hojas: Nodos que no tienen hijos (que no sale ninguna "flecha")
- No tiene _Ciclos_ ;)
## Visualizando Grafos
Una forma bastante cómoda y sencilla para visualizar grafos es el formato [DOT: graph description language](https://en.wikipedia.org/wiki/DOT_%28graph_description_language%29 target="_blank")
La gran ventaja de este formato es que es simplemente un archivo de texto, con lo que podremos generarlo fácilmente desde nuestro código y luego visualizarlo.
Un ejemplo
fichero: mygraph.dot
~~~~~~~~~~~~~~~~ dot
digraph G {
node_a -> node_c
node_b -> node_d
node_c -> node_d
node_d -> node_f
node_e -> node_f
}
~~~~~~~~~~~~~~~~
Una vez tenemos ese fichero de texto podemos visualizar el grafo simplemente con
usar el comando _dot_ de [GraphViz](http://www.graphviz.org/ target="_blank")
~~~~~~~~~~~~~~~~~ bash
# uso: dot -T[Formato de imagen] fichero.dot -o [fichero_imagen_salida].
$ dot -Tpng mygraph.dot -o mygraph.png
~~~~~~~~~~~~~~~~~
y tendremos este resultado:
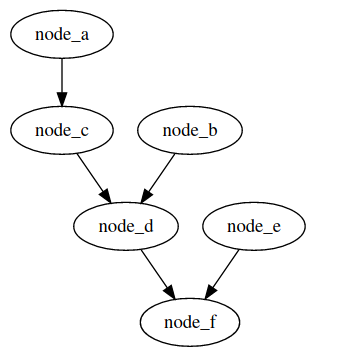
!!! Tip
Si no quieres instalarte este software, puedes usar la versión online [webGraphViz](http://webgraphviz.com/ target="_blank").
## Programando Grafos
Bueno, vamos a suponer que ya tenemos algo más claro lo que son los grafos y lo útiles que son a la hora de definir sistemas.
Ahora es momento de empezar a hablar de la implementación.
Para trabajar con grafos las operaciones más comunes que debemos tener implementadas son:
~~~~~~~~~
add_node(i): Agrega un Nodo al grafo, identificado por i.
add_edge(i,j): Agrega una Arista del Nodo i al Nodo j.
remove_edge(i,j): Elimina una Arista de i a j.
has_edge(i,j): Comprueba si hay una Arista del Nodo i a j.
out_edges(i): Devuelve los Nodos hijos del Nodo i.
in_edges(i): Devuelve los Nodos padre del Nodo i.
to_dot(): Función que genera un string con la definición del grafo en formato DOT.
~~~~~~~~~
Para implementar un DAG se pueden utilizar varias técnicas pero las más comunes son:
### Matriz de adyacencia
Una de las formas más comunes de representar el grafo es hacerlo como una matriz. Estas se implementan con una matriz de NxN siendo N el numero de nodos.
Cada posición de i,j de la matriz representa una arista ( flecha ) del nodo i al nodo j.
Se podría expresar así:
$$ a_{i,j}\begin{cases}true & i\rightarrow j \\false & i\nrightarrow j \end{cases} $$
Y podríamos verlo así
$$
\begin{matrix}&a &b &c &d &e &f\cr
a & 0&0&1&0 &0 &0\cr
b & 0&0 &0 &1 &0 &0\cr
c & 0&0 &0 &1 &0 &0\cr
d & 0& 0 & 0 & 0 & 0 &1\cr
e & 0& 0 & 0 & 0 & 0 &1\cr
f & 0& 0 & 0 & 0 & 0 &0\cr
\end{matrix}
$$
Esta implementación tiene la ventaja de que las operaciones de agregar, eliminar y comprobar si dos nodos están conectados tiene coste constante y son triviales
~~~~~~~~~~~~~~ cpp
#pseudo-código para agregar un vértice del Nodo i al Nodo j
bool add_edge(i,j){
return adj_matriz[i][j]==true;
}
~~~~~~~~~~~~~~
La implementación de las funciones para conocer los "familiares" (Nodos padres e hijos) son bastantes sencillas pero, a la vez, tienen un coste mayor
~~~~~~~~~~~~~~ cpp
# pseudo-código para extraer los hijos de un nodo
lista out_edges(i){
lista out;
for(j=0; j < num_nodos; j++)
{
if( adj_matriz[i][j] )
out.append(j)
}
return out
}
# piensa tu como hacer la implementación de in_edges
in_edges(i){
...
}
~~~~~~~~~~~~~~
La gran problemática con este enfoque es que para recorrer el grafo deberemos ejecutar constantemente estas funciones, que tienen un coste lineal, O(n).
Además el coste en memoria es n², algo que podría ser un problema para grafos grandes.
### Lista de adyacencias
Otro enfoque para trabajar con grafos es el usar una lista con la lista de Nodos hijo de cada nodo.
$$
\\
a \rightarrow [c] \\
b \rightarrow [d,c] \\
c \rightarrow [d] \\
d \rightarrow [d] \\
e \rightarrow [f] \\
f \rightarrow [] \\
$$
El coste de estas implementaciones depende mucho del contenedor que se use para almacenar las aristas y de como se haya implementado en el lenguaje elegido, pero también ofrece mucha más versatilidad.
Como ejemplo, si usamos una lista se podría implementar así:
~~~~~~~~~~~~~~ cpp
# pseudo-código para agregar un vértice del nodo i al nodo j
add_edge(i,j){
adj_list[i].append(j);
}
~~~~~~~~~~~~~~
La implementación de las funciones para conocer los "familiares" (Nodos padres e hijos) son bastantes sencillas.
~~~~~~~~~~~~~~ cpp
# pseudo-código para extraer los hijos de un nodo
lista out_edges(i){
return adj_list[i];
}
# piensa tu como hacer la implementación de in_edges
lista in_edges(i){
...
}
~~~~~~~~~~~~~~
!!! Note
También se puede implementar usando multilistas, o lo que es lo mismo una lista que tiene los padres de un nodo y otra lista que contenga los hijos de ese nodo.
# Implementando el grafo.
## Inciso antes de empezar.
Una vez visto esto por encima, vamos a hacer un pequeño inciso para comentar como vamos a trabajar en estos posts.
En los posts se irá explicando la teoría y dando algunos ejemplos, pero la solución final deberéis programarla vosotros.
Para daros una guía en la que apoyarse haremos un enfoque parecido a TDD (Test Driven Development), así que os plantearé unos test unitarios para que podáis probar vuestro código.
!!! Info
Habrá un repositorio en github (*con errores para evitar C&P*) mostrando una posible implementación en C++.
## Implementando que es gerundio.
En este primer ejercicio vamos a implementar un DAG.
Tenéis libertad absoluta para elegir si queréis usar una matriz de adyacencia, o una lista, o simplemente nodos con referencias a otros nodos.
El pseudo-código estará expuesto como si fuéramos a implementarlo con clases, pero repito,tenéis libertad absoluta para implementarlo como queráis.
Para nuestra primera aproximación vamos a hacer un grafo que sea capaz de ejecutar las operaciones básicas con grafos que ya hemos comentado.
Vamos a tener un Objeto Node que tenga algo de funcionalidad.
~~~~~~~~~~~~~~~~~~
# pseudo-código definición de grafo
struct Node{
string node_name;
// constructor, asigna name a node_name
Node(name);
// devuelve el nombre del nodo (node_name).
get_name();
;}
class graph{
tipo_contenedor nodes; // un contenedor donde almacenar los nodos
add_node(node_name):
add_edge(i,j);
remove_edge(i,j);
has_edge(i,j);
out_edges(i);
in_edges(i);
to_dot(); // helper para exportar todas las relaciones del grafo a un formato texto DOT ( a un string)
}
~~~~~~~~~~~~~~~~~~
Una vez hayas implementado tu grafo vamos a tener que probarlo, así que vamos a definir unos tests que deben pasarse correctamente.
Puedes hacerlos a mano o usar un framework de unittesting.
~~~~~~~~~~~~~~~~~~~~ cpp
// Test creación de grafo en pseudo-código
graph g;
g.add_node(node_a);
g.add_node(node_b);
g.add_node(node_c);
g.add_node(node_d);
g.add_node(node_e);
g.add_node(node_f);
g.add_edge(node_a,node_c);
g.add_edge(node_b,node_d);
g.add_edge(node_c,node_d);
g.add_edge(node_d,node_f);
g.add_edge(node_e,node_f);
print ( g.to_dot() );
~~~~~~~~~~~~~~~~~~~~
Si todo está correcto os debería haber generado un grafo como este:

Recordad que podéis probar vuestro resultado en la versión [web de GraphViz](http://webgraphviz.com/ target="_blank").
~~~~~~~~
//Resultado del test anterior.
digraph G {
node_a -> node_c
node_b -> node_d
node_c -> node_d
node_d -> node_f
node_e -> node_f
}
~~~~~~~~
Otras pruebas que deben pasar vuestra implementación.
~~~~~~~~~~~~~~~~~~~~ cpp
// Test manipulación de grafo en pseudo-código
graph g;
g.add_node(node_a);
g.add_node(node_b);
g.add_node(node_c);
g.add_node(node_d);
g.add_node(node_e);
g.add_node(node_f);
g.add_edge(node_a,node_c);
g.add_edge(node_b,node_d);
g.add_edge(node_c,node_d);
g.add_edge(node_d,node_f);
g.add_edge(node_e,node_f);
//Test función has_edge
assert(g.has_edge(node_a,node_b)==false);
assert(g.has_edge(node_b,node_d)==true);
//Test remove edge
g.remove_edge(node_b,node_d);
assert(g.has_edge(node_b,node_d)==false);
~~~~~~~~~~~~~~~~~~~~
Bueno, ahora ya has sido capaz de implementar las manipulaciones básicas de un grafo, así que vamos a empezar a trabajar con ellos.
# Algoritmos sobre grafos
Una vez tenemos la capacidad de manipular grafos algo que necesitaremos constantemente será recorrerlos y no solo como nodos independientes si no siguiendo el orden definido en el grafo y pasando por cada nodo *exactamente* una vez.
Y el orden en que se visitan los vértices es importante y depende del problema que quieres resolver.
Los métodos más comunes para recorrer un grafo son el DFS (Depth First Search) y BFS (Breadth First Search).
Haciendo un poco de spoiler, os avanzo que nosotros usaremos BFS constantemente :).
## DFS (Depth First Search)
El DFS empieza desde un nodo del grafo y lo visita. Una vez visitado, saltamos a cada uno de los padres de este nodo, y repetimos la operación.
La versión iterativa de este algoritmo usa una Pila (LIFO) a la que agregamos el nodo inicial y empezamos a sacar elementos de la pila.
por cada elemento, agregamos sus padres a la Pila, lo visitamos y volvemos al loop.
~~~~~~~~~ cpp
# DFS en pseudo-código
lista_nodes DFS (node_i){
stack S; // recordar que es un contenedor LIFO
lista visited;
S.push( node_i ) //Insertamos el nodo inicial en el stack
visited.append(node_i)
while ( S.empty() == false){
v = S.pop( )
visited.append(v)
for( w in in_edges(v) )
if w is not in visited
{
S.push( w )
}
}
return visited; //devolvemos la lista de los nodos en el orden profundo correcto
}
~~~~~~~~~
Visualmente es más sencillo de ver.

!!! Info
El orden en que se agregan los vértices es importante, ya que depende de como los agreges recorrerá los padres de distinto orden.
El resultado es igualmente correcto, pero a nivel de Test Unitarios puede daros más de un dolor de cabeza.
### Tests unitarios
Ahora os toca a vosotros implementar este BFS en vuestros grafos, aquí tenéis un test para comprobar que os funciona correctamente.
~~~~~~~~~~~~~~~~~~~~ cpp
// Test DFS en pseudo-código
graph g;
g.add_node(node_a);
g.add_node(node_b);
g.add_node(node_c);
g.add_node(node_d);
g.add_node(node_e);
g.add_node(node_f);
g.add_node(node_g);
g.add_node(node_h);
g.add_node(node_i);
g.add_node(node_j);
// el orden en que se agregan los vértices es importante para que salga el resultado que queremos.
// aunque el resultado final sea correcto, el orden puede variar.
g.add_edge(node_j, node_h)
g.add_edge(node_i, node_h)
g.add_edge(node_h, node_a)
g.add_edge(node_g, node_a)
g.add_edge(node_f, node_b)
g.add_edge(node_e, node_c)
g.add_edge(node_d, node_c)
g.add_edge(node_c, node_b)
g.add_edge(node_b, node_a)
//Test DFS
resultado = g.dfs(node_a)
assert(resultado == [node_a,node_b,node_c,node_d,node_e,node_f,node_g,node_h,node_i,node_j])
~~~~~~~~~~~~~~~~~~~~
## BFS (Breadth First Search)
Otra forma de recorrer un grafo es la conocida como Breadth First Search (BFS). En esta variación usamos un proceso similar al DFS pero en lugar de usar una pila usaremos una cola (FIFO).
Al usar esta cola, el algoritmo cambia ligeramente.
El BFS empieza desde un nodo del grafo, lo visita y agrega sus padres a la cola. Una vez visitado, saltamos a cada uno de los padres de este nodo y repetimos la operación.
La versión iterativa de este algoritmo usa una cola (FIFO) a la que agregamos el nodo inicial y empezamos a sacar elementos de la cola. Por cada elemento, agregamos sus padres a la cola, lo visitamos y volvemos al loop.
~~~~~~~~~ cpp
class graph{
...
lista_nodes BFS (node_i) {
queue Q; // recordar que es un contenedor FIFO
lista visited;
Q.push( node_i ); //Insertamos el nodo inicial en la cola
visited.append(node_i)
while( Q.empty() == false)
{
v = Q.pop( )
//procesamos todos los padres de v
for( w in in_edges(v) )
if w is not in visited
{
Q.push( w )
}
}
return visited; //devolvemos la lista de los nodos en el orden transversal correcto
}
~~~~~~~~~

### Tests unitarios
Ahora os toca a vosotros implementar este BFS en vuestros grafos, aquí tenéis un test para comprobar que os funciona correctamente.
~~~~~~~~~~~~~~~~~~~~ cpp
// Test BFS en pseudo-código
graph g;
g.add_node(node_a);
g.add_node(node_b);
g.add_node(node_c);
g.add_node(node_d);
g.add_node(node_e);
g.add_node(node_f);
g.add_node(node_g);
g.add_node(node_h);
g.add_node(node_i);
g.add_node(node_j);
g.add_edge(node_d,node_c);
g.add_edge(node_e,node_c);
g.add_edge(node_c,node_b);
g.add_edge(node_b,node_a);
g.add_edge(node_g,node_a);
g.add_edge(node_h,node_a);
g.add_edge(node_f,node_b);
g.add_edge(node_i,node_h);
g.add_edge(node_j,node_h);
//Test BFS
resultado = g.bfs(node_a)
assert(resultado == [node_a,node_b,node_g,node_h,node_c,node_f,node_i,node_j,node_d,node_e])
~~~~~~~~~~~~~~~~~~~~
Enhorabuena!
Ya has implementado una gran parte de la funcionalidad necesaria para trabajar con grafos en cualquier problema.
Pero esto no acaba aquí, ahora os voy a proponer 2 problemillas que deberéis solucionar vosotros solos.
El primero (Reverse BFS) es bastante importante que lo penséis, el segundo es un bonus track.
# Deberes ;)
## Reverse BFS
Ahora que ya tenemos una forma de recorrer nuestros grafos tenemos que pensar en una funcionalidad que vamos a necesitar para nuestra librería de Deep Learning.
El reverse BFS, y esto no es mas que saber la lista de nodos para recorrer el grafo como se hace en un BFS, pero en dirección contraria.
Si nuestro BFS nos devuelve una lista de [1,2,3,4], nosotros deberemos recorrerla como [4,3,2,1]
Intentad implementarlo :).
### Tests unitarios
~~~~~~~~~~~~~~~~~~~~ cpp
// Test Reverse BFS en pseudo-código
graph g;
g.add_node(node_a);
g.add_node(node_b);
g.add_node(node_c);
g.add_node(node_d);
g.add_node(node_e);
g.add_node(node_f);
g.add_node(node_g);
g.add_node(node_h);
g.add_node(node_i);
g.add_node(node_j);
g.add_edge(node_d,node_c);
g.add_edge(node_e,node_c);
g.add_edge(node_c,node_b);
g.add_edge(node_b,node_a);
g.add_edge(node_g,node_a);
g.add_edge(node_h,node_a);
g.add_edge(node_f,node_b);
g.add_edge(node_i,node_h);
g.add_edge(node_j,node_h);
//Test BFS
resultado = g.reverse_bfs(node_a)
assert(resultado == [node_e,node_d,node_j,node_i,node_f,node_c,node_h,node_g,node_b,node_a])
~~~~~~~~~~~~~~~~~~~~
# Para nota.
## Detectar ciclos en tu Digrafo
Os comento que con el DFS se pueden detectar ciclos en un DAG, ¿se te ocurre una manera de detectar si un grafo es un DAG o no?
Intentaló y pruébalo.
### Tests unitarios
~~~~~~~~~~~~~~~~~~~~ cpp
// Test Reverse BFS en pseudo-código
graph g;
g.add_node(node_a);
g.add_node(node_b);
g.add_node(node_c);
g.add_node(node_d);
g.add_node(node_e);
g.add_node(node_f);
g.add_node(node_g);
g.add_node(node_h);
g.add_node(node_i);
g.add_node(node_j);
g.add_edge(node_d,node_c);
g.add_edge(node_e,node_c);
g.add_edge(node_c,node_b);
g.add_edge(node_b,node_a);
g.add_edge(node_g,node_a);
g.add_edge(node_h,node_a);
g.add_edge(node_f,node_b);
g.add_edge(node_i,node_h);
g.add_edge(node_j,node_h);
//Test BFS
assert (g.is_DAG(node_a) == True)
graph g2;
g2.add_node(node_1)
g2.add_node(node_2)
g2.add_node(node_3)
g.add_edge(node_1,node_3);
g.add_edge(node_2,node_3);
g.add_edge(node_3,node_2);
//Test BFS
assert (g2.is_DAG(node_1) == False)
~~~~~~~~~~~~~~~~~~~~
# Repositorio
Todo el código y ejemplos los podréis encontrar en el
[Repositorio GitHub]("https://github.com/anlismon/DeepLearningFromScratch" target="_blank").
# Siguientes pasos
En el próximo post hablaremos de Álgebra.
Álgebra pura y dura.
Pero no os asustéis demasiado, no será muy doloroso ;)
# Dudas y preguntas.
Si tienes cualquier duda, pregunta o he metido la pata en algún sitio, puedes contactar conmigo en twitter:
-------------------------